Coordination
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, Universityof Wisconsin - Green Bay
Coordination
Coordination polyhedra are dictated by the relative sizes of the cation and the anion. Consider a silica tetrahedron again. If we remove the silicon and insert a smaller cation,the structure may be stable, although the cation might rattle around a bit. But eventually the cation will be so tiny that it can pull three anions around itself and squeeze the fourth one out entirely. On the other hand, if we insert a bigger cation, it will push the anions apart. Eventually it will create enough extra room that an additional anion or more can be pulled in. So each coordination polyhedron is (theoretically) stable only within certain geometrically-defined radius limits.
However, real crystals aren't as simple. To obtain a different coordination number, a cation has to pull anions away from other cations. Whether that can happen will depend on the numbers of cations, their radii and charges, extent of covalent bonding, and so on. Studies of real crystals show that most of the time coordination number corresponds to the theoretical geometrical limits but there are exceptions at both the upper and lower limits.
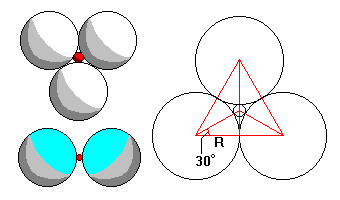 |
Left: very tiny cations (bottom) only have room for two adjoining anions, but slightly larger cations force anions apart enough to allow threefold coordination (top).
Right: If R is the larger ionic radius and r the smaller, we can see that (R+r) cos 30 = R, or (1+r/R) cos 30 = 1, or r/R = (1-cos30)/cos 30 = 0.155 |
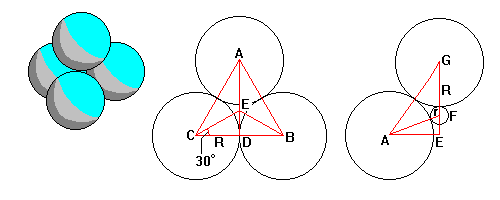 |
Fourfold (tetrahedral) coordination is the hardest case to visualize coordination criteria. The center diagram shows the base of the tetrahedron and the right diagram shows a cross-section through the apex. |
In the center diagram, AE = CE = R/cos30=1.1547R (This equals 1/3 AD). On the right diagram sinG = AE/AG = 1.1547/2 = 0.5773. Cos G = 0.8165 = R/(R+r). Thus 1 + r/R =1/0.8165 = 1.225 and r/R = 0.225.
Since AG = 2R and cosG = 0.8165, EG = AG cosG = 1.633R. Now GF = R+r = 1.225 R, so EF=0.408R=EG/4.
Since tetrahedra crop up so often in crystallography, these are two handy tidbits to remember: DE=AD/3 and EF=EG/4. Both relations are exact.
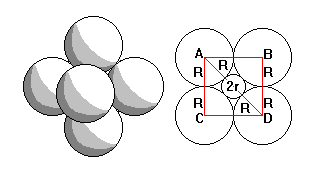 |
Six-fold coordination has a simple radius criterion. AD = 2(R+r) and AB = 2R=ADcos45. So 2R=2Rcos45+2rcos45 and
r/R=(1-cos45)/cos45=0.414 |
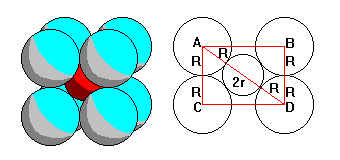 |
Eight-fold coordination also has a simple radius criterion. AB=2Rsqrt(2) and AD=2Rsqrt(3)=2R+2r. So 2r=2R(sqrt(3)-1) and r/R=(sqrt(3)-1)=0.732 |
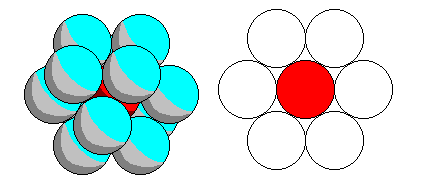 |
Twelve-fold coordination is easiest of all. r/R=1. |
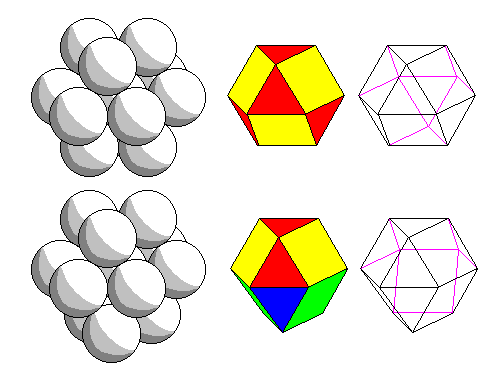 |
Top: for cubic close packing, the coordination polyhedron is a solid with square and triangular faces called a cuboctahedron. It can be derived equally by truncating the vertices of a cube or an octahedron.
Bottom: for hexagonal close packing, the coordination polyhedron is similar to the cuboctahedron, but the bottom half is rotated 60 degrees. The resulting solid has only three-fold symmetry. |
Other coordination geometries are possible, though less common.
Return to Mineralogy-Petrology Index
Return to Thin-Section Index
Return to Crystals and Light Index
Return to Crystal Structures Index
Return to Mineral Identification Tables
Return to Professor Dutch's Home Page
Created 18 September 1999, Last Update