Density and Atomic Arrangements
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, University of Wisconsin - Green Bay
Density is a good illustration of the way macroscopic properties of materials can be described in accurate detail by their atomic properties. Halite or table salt, NaCl, gives us a particularly simple illustration. The atoms in halite are arranged in a cubic pattern as shown below:

The spacing between Cl atoms is 5.64 Angstrom Units or 0.564 nm
It's obvious that the most fundamental cube (unit cell) of halite contains more than one Na and one Cl atom, but how many? If we zoom in for a closer look we see that atoms are shared between adjacent cubes, complicating matters further. There are three atomic layers in each cell and they look as shown below. In the diagrams, the Na and Cl symbols repeat only to show how atoms are shared. There are only nine atoms in each diagram: at the corners, midpoints of edges, and center of each square.
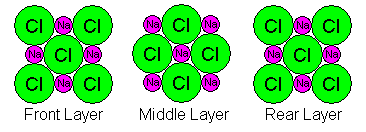
- The front layer layer also shares atoms with the layer in front of it. Thus we have 1/8 of the four corner Cl atoms plus half of the center one: 4(1/8)+1/2 = 1. Also, we have 1/4 of the four shared Na atoms: 4(1/4)=1.
- In the middle layer we have 1/4 of the four corner Na atoms plus the central one: 4(1/4)+1=2. Also we have half of four Cl atoms: 4(1/2)=2.
- The rear layer also shares atoms with the layer behind it. Thus we have 1/8 of the four corner Cl atoms plus half of the center one: 4(1/8)+1/2 = 1. Also, we have 1/4 of the four shared Na atoms: 4(1/4)=1.
Thus we have one Na and Cl atom in the front layer, two in the middle, and one in the back, for a total of four. Our tendency to draw unit cells with atoms at the corners actually complicates matters. If we draw the unit cell boundariesbetween the atoms, we actually get a much simpler picture as shown below. However, sometimes it's necessary to count atoms as shared, so it's important to be able to do it either way.
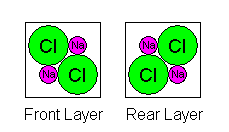 |
Here it is obvious we have four sodium atoms and four chlorines in a unit cell. |
The volume of the unit cell is (5.64 x 10-8) cm, cubed, or1.794 x 10-22 cubic centimeters. The atomic weight of Na is 23 and Cl is 35.45. The total molecular weight of the atoms in a unit cell is 4(23 + 35.45) = 233.8.
How do we convert that to grams? A mole of sodium weighs 23 grams and contains 6.02 x1023 atoms (Avogadro's Number) so a single atom weighs 23/(Avogadro's Number) grams. Thus the mass of all the atoms in a unit cell is 233.8/(Avogadro's Number) = 3.884 x10-22 grams.
Fact worth Remembering: The mass of any atom or molecule in grams is its atomic or molecular weight divided by Avogadro's Number.
The density of halite, then, should be mass divided by volume, or
(3.884 x 10-22)/(1.794 x 10-22) = 3.884/1.794 = 2.165 grams per cubic centimeter.
This agrees very closely with the tabulated value. Actual densities may vary slightly because of impurities but for pure materials, the calculated density should agree with the observed density to very high precision.
The ionic radius of Na(+1) is 0.98 Angstrom units, that of Cl(-1) is 1.81. The width of a cube is two ionic radii of Na plus two of Cl, or 2(0.98+1.81) = 2(2.79) = 5.58 Angstrom units. This is a gratifyingly close match to the measured value. It's not exact because the effective radius of an ion varies a bit depending on the other atoms around it, and some ions, especially the semi-metals, behave as if they're ellipsoidal. At the atomic level we begin seeing quantum effects that complicate our macroscopic concepts of reality. Nevertheless, it's amazing how far you can go in crystallography by treating atoms as rigid spheres.
"Theory" is not some vague, arm-waving notion divorced from reality. Theories are supposed to match observation exactly. If they don't, it's because the theory is imperfect, or the observational data is inaccurate. When both the data and the theory are sound, they should match to high precision, as they do here.
Return to Mineralogy-Petrology Index
Return to Thin-Section Index
Return to Crystals and Light Index
Return to Crystal Structures Index
Return to Mineral Identification Tables
Return to Professor Dutch's Home Page
Created 18 September 1998, Last Update