Kamacite and Taenite
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, Universityof Wisconsin - Green Bay
Kamacite and Taenite are the principal iron-nickel alloy minerals in iron meteorites. Taenite is the nickel-rich phase (mnemonic: Taenite contains "ni") with 30 to 70 per cent nickel. Kamacite is the iron rich phase with generally 5-10 per cent nickel.
Iron and nickel are chemically similar and their atoms in the metallic state are very similar in size, so it would seem like they should form a complete solid solution series. However, for reasons rooted in quantum mechanics and magnetism, nickel has a face centered lattice and iron at room temperature has a body centered lattice. At high temperatures, iron also assumes a face centered structure, a variety called austenite. Just to complete the trilogy, cobalt, the intervening element, has a hexagonal close-packed structure.
Taenite essentially has a nickel lattice and kamacite has an iron lattice. At high temperatures both iron and nickel are face-centered, and iron meteorites are essentially all taenite. As the temperature drops, kamacite begins to exsolve, expelling nickel into the taenite and forming thin lamellae of almost pure iron. The most common variety of iron meteorite is called "octahedrite" because the kamacite lamellae are oriented along the octahedral {111} faces of the taenite. The crystallographic plane that dominates in the kamacite lamellae is the {101} plane, but the alignment between the two planes is only approximate.
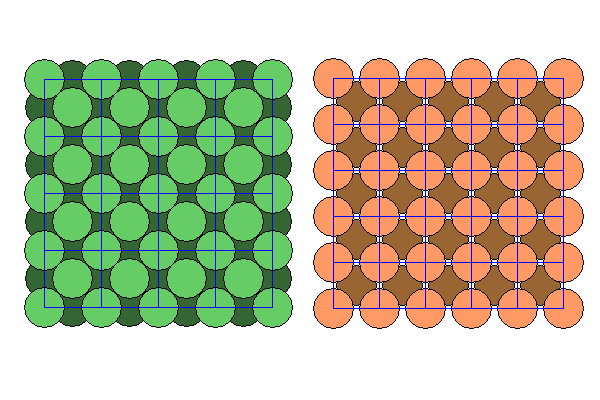
Above we see the taenite structure (left, in green) and the kamacite structure (right, in orange). These are essentially the same as the nickel and iron lattices and the atoms are very similar in size. Note that the unit cell dimension ratio is very nearly 5:4
To see how kamacite and taenite are related in meteorites, we will first need to determine some lattice dimensions. So lattice calculate (lattice - let us?). Let the radius of an iron or nickel atom equal 1. In taenite it is obvious that the diagonal of a unit cell face is 4, and also equal to sqrt(2) ef, the unit cell edge. So ef = 2sqrt(2) =2.828 .
The unit cell for kamacite is a bit harder to visualize. Here, the atoms form continuous chains along the long diagonals of the unit cells. The long diagonal has length 4 = sqrt(3) eb, or eb = 4sqrt(3)/3 = 2.309. Note that 2.828/2.309 = 1.224, not too different from 1.25 = 5/4.
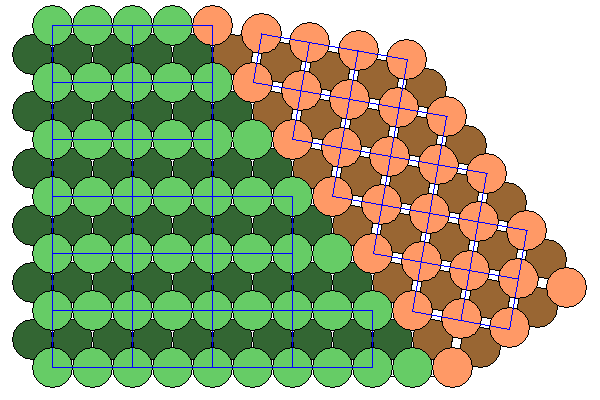
Above is a diagram of the relationship between kamacite and taenite. Here we are looking along the {111} plane of taenite, or a cross section diagonally through the unit cells. The kamacite is joined to the taenite along the {111} plane of taenite and the {101} plane of kamacite.
How good is the fit? The diagonal of the kamacite unit cell is ebsqrt(2) = 3.265. The atoms on the taenite {111} face are distance ef apart vertically and (sqrt(2)/2)ef horizontally, so the distance between atoms in the taenite {111} plane is sqrt(2)(5/4)ef = 1.118ef = 3.162 (actually works out exactly to sqrt(10)). So the misfit is about 3 per cent, good enough to allow the two lattices to join but big enough to require adjustments before terribly long. Hence the observations that the alignment is more approximate than exact.
Return to Mineralogy-Petrology Index
Return to Thin-Section Index
Return to Crystals and Light Index
Return to Crystal Structures Index
Return to Mineral Identification Tables
Return to Professor Dutch's Home Page
Created 15 October 2009, Last Update