Metamorphic Phase Diagrams
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, Universityof Wisconsin - Green Bay
The Phase Rule
The Phase Rule is P + F = C + 2, where
- P = number of phases present
- F = Degrees of freedom,
- C = number of components present
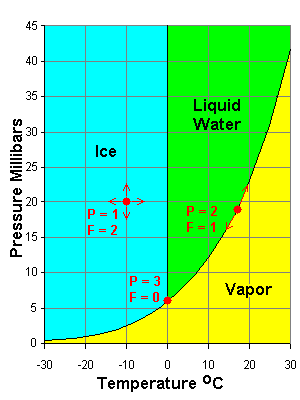
The familiar systems below illustrate the phase rule. In both cases, C = 1 so P + F = C + 2 = 3.
 |
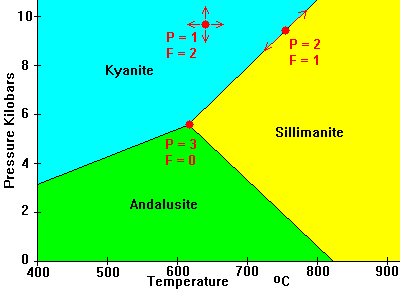 |
- In the middle of a field, we can vary temperature and pressure at will (within limits); There is only one phase (P = 1) and F = 2.
- On a phase transformation boundary, two phases are present but we only have one degree of freedom. If we modify pressure we have to change temperature to stay on the boundary. If we modify both temperature and pressure at will we move off the boundary into a region where F = 2 but P = 1.
- At the triple points we have all three phases present but no freedom at all. We have to be at that temperature and pressure to have all three phases present; F = 0
The phase rule applies only to chemical systems in equilibrium. It plays very little role in sedimentary petrology, where rocks consist of diagenetic minerals that may be in equilibrium, but also detrital minerals that may be wildly out of equilibrium. It may play a role at times in igneous petrology, but igneous rocks are often non-equilibrium because crystals may be zoned or rimmed and their interiors isolated from the rest of the magma. The phase rule figures prominently in metamorphic petrology, where equilibrium is commonly the rule.
What constitutes a component is sometimes a matter of definition, for example, if a component is always present, we may simply ignore it. If a rock contains Al2SiO5 and quartz, we might choose to ignore the quartz, if it doesn't participate in any chemical reactions. Or we might choose to count quartz as a phase, in which case we must also count SiO2 as a component. We don't need to consider Al2O3 and SiO2 as separate components if they always occur as Al2SiO5. However, if there were the possibility that quartz or corundum might occur as well, then we would have to consider Al2O3 and SiO2 as separate components.
Most of the time F = 2; temperature and pressure. Occasionally F can be greater, for example if total pressure and water pressure are different, or if the relative pressures of water and carbon dioxide are important, or if oxidation potential is important.
If F = 2 then P + 2 = C + 2 and P = C.
We see this to some extent in calculating norms for igneous rocks; titanium is assumed to go into titanite or ilmenite, phosphorus into apatite, and so on. For each component, there is a phase.
Metamorphic Phases and Phase Diagrams
In metamorphic rocks, we need to consider these important components: SiO2, Al2O3, FeO,Fe2O3, CaO, Na2O, K2O, MgO, TiO2 and H2O. The most components we can conveniently deal with at one time is only three, on a triangle plot. Ten components, taken in threes, makes for (10*9*8)/(1*2*3) = 120 triangle plots. Nobody has ever plotted phase diagrams in that sort of detail.
We can simplify by making certain simplifying assumptions:
- TiO2 goes predictably into rutile or sphene
- Fe2O3 is uncommon (deep in the crust conditions are not very oxidizing) and usually either goes into hematite or magnetite, or substitutes for Al.
- MgO substitutes for FeO
- We can usually assume water is present in excess and ignore it as a separate component, or assume it is absent in very anhydrous rocks.
- We treat carbon dioxide much the same way: assume it's present to excess in carbonate rocks and absent otherwise.
Thus we simplify to the following components: (SiO2), (Al2O3), (FeO + MgO), CaO, Na2O,and K2O. Thus C = 6, which means (if F = 2) that P = 6. Most metamorphic rocks typically contain 5 or 6 main mineral phases. Minor components like Cr, or P usually have their own phases (chromite and apatite, respectively).
With a few further simplifying assumptions, we can reduce C to 3 and plot the systems on triangle plots. Among the most common assumptions:
- SiO2 is always present as quartz (true except for extremely silica-poor rocks)
- Na2O always occurs as albite (true except for extreme high-pressure or very sodic assemblages)
- K2O is always present as muscovite or K-feldspar
- CaO occurs as plagioclase or calcite
By applying these simplifying assumptions appropriately, we can describe many metamorphic rocks in terms of three variable components (which we're interested in) and three background components that are always accounted for in certain ways (which we ignore).
Limitations of Simplifying Assumptions
- Mn can sometimes form spessartine garnet.
- Na can occur as riebeckite or paragonite in Na-rich rocks, or glaucophane and jadeite in high-pressure assemblages.
- FeO and MgO are not totally free to substitute. Mg and Fe phases are plotted separately on the AFM diagram.
- Al can go into garnet or tourmaline (if B is present).
- Minerals do not have simple, ideal compositions
- Mineral composition depends on the bulk chemistry of the rock.
Principal Types of Phase Diagrams
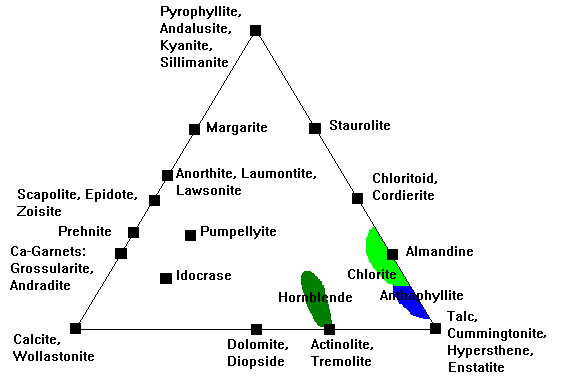
The ACF Diagram
In the ACF diagram, we assume K always goes into feldspar or mica, Na into albite, and quartz is present. That leaves Al, Ca and Fe-Mg to account for. We define:
- A = (Al2O3 + Fe2O3)- (K2O + Na2O). Note that even though we don't count K or Na as components, we do have to account for the fact that Al goes into feldspar and mica along with them.
- C = CaO - 3.3 P2O5 (Correction for calcium in apatite, which we otherwise ignore.)
- F = (FeO + MgO)
The A'KF Diagram
In the A'KF diagram, we track Al, K and Fe-Mg. We define:
- A' = (Al2O3 + Fe2O3)- (K2O + CaO + Na2O). Again, we account for the fact that Al goes into feldspar and mica along with the alkali metals.
- K = K2O
- F = (FeO + MgO)
This diagram is often paired with the ACF diagram, and all the minerals on the A'-F edge plot in the same places. Thus, many references show this diagram point-down.
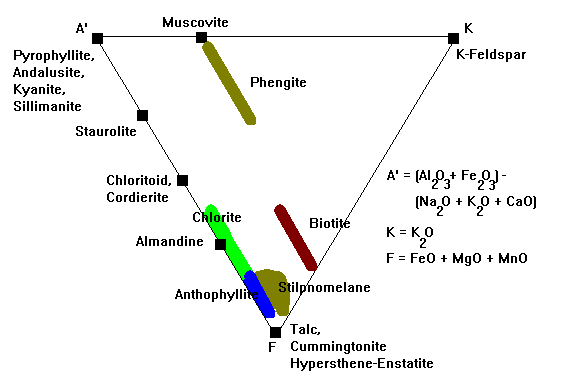
Phengite is muscovite with substantial Mg and Fe, stable at low temperatures and high pressures.
The AFM Diagram
This diagram attempts to deal with the fact that Fe and Mg do not fully substitute for one another. Many of the ferromagnesian minerals also contain Al, but biotite also contains K. Thus, we have to track four components in a tetrahedron. We do this by assuming that muscovite is always present in these rocks, picking the muscovite point as our projection point, then projecting everything onto the AFM plane. Note that some points plot inside the AFM triangle and some outside.
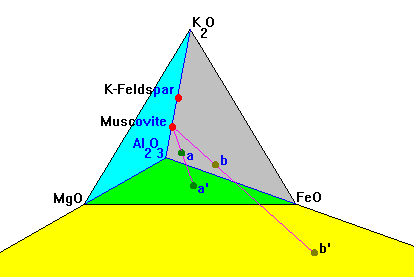 |
In this diagram, composition a plots at a' inside the Al-Mg-Fe triangle but b plots at b', outside it.
K-feldspar is usually said to plot at infinity on this plot but in reality it never plots on the AFM plane at all. |
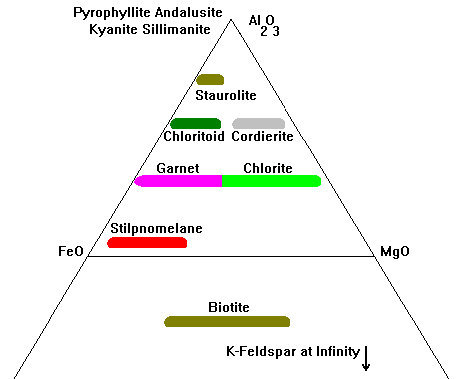 |
Principal minerals tracked on this plot are shown here. Al2O3 is usually occupied by pyrophyllite, andalusite, kyanite or sillimanite.
Mg-Fe silicates like olivine, enstatite-hypersthene, anthophyllite, and so on would plot along the Mg-Fe line but this diagram is almost never used for rocks where these minerals would occur. |
Virtually every text describes and uses this diagram wrong! Mineral assemblages, as in all other phase diagrams, are indicated with tie lines joining coexisting minerals. Since all of these minerals have very variable compositions, the diagrams are typically shown with fanning bundles of tie lines connecting the range of compositions of one mineral with that of another. It's either said or implied that the tie line joins the composition of one mineral to the corresponding composition of the other.
A little thought will suffice to show that this is almost never true. For one thing, there simply isn't enough compositional data in many cases to support such a claim. If such data did exist, the tie lines would have to be precisely plotted based on actual data and would be identical from diagram to diagram. They never are. For another, as the relative amounts of Fe, Mg and Al vary, tie lines can never sort out cleanly - tie lines joining say, stilpnomelane, biotite and chlorite in one rock will almost certainly cross tie lines to these minerals in other, slightly different rocks.
Rather than continue the misleading tradition of tie line bundles, which is visually cluttered and geologically meaningless anyway, it seems far more preferable simply to draw a single tie line from the average composition of one phase to the average of any other phase.
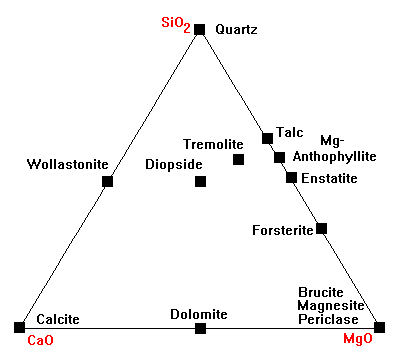
The CaO-MgO-SiO2 Diagram
This is the standard diagram for dealing with carbonate rocks.
Evolution of Phase Diagrams
Since P + F = C + 2, and C = 3, then P + F for a standard metamorphic triangle plot is equal to 5. Normally, in any stability field of a phase diagram, 3 phases are present and there are 2 degrees of freedom, usually temperature and pressure. When a reaction is at equilibrium, we are on some T-P reaction curve and the number of degrees of freedom drops to one. (If we vary temperature, we also have to vary pressure to stay on the T-P reaction curve. If we depart from the reaction curve at all, the chemical reaction will run in one direction or the other to completion.) Thus, while a reaction is in progress, F = 1 and P= 4. We can have 4 phases present in one of several ways:
- We can dissolve a tie line, creating a quadrilateral with 4 phases at its vertices. As the reaction runs to completion, the quadrilateral is divided by the other diagonal than the one that was dissolved.
- A new phase can appear in the interior of a field. As the reaction runs to completion, new tie lines will join the new phase to the vertices of the field and a formerly single field will be trisected.
- A new phase can appear on the boundary of a field. As the reaction runs to completion, a new tie line will join the new phase to the opposite vertex of the field and a formerly single field will be bisected.
The low-temperature metamorphism of carbonate rocks illustrates these possible changes:
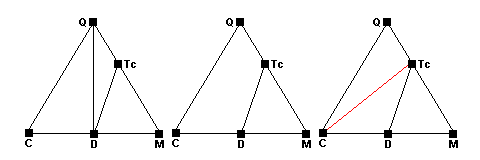
The left-hand diagram shows the normal carbonate sedimentary assemblage. the phases represented are quartz (Q), calcite (C), dolomite (D) and magnesite (M). Around 400 C, talc forms via the reaction 3Mag + 4Qz + H2O = Tc + 3CO2. The newpoint representing talc (red) forms along the Q-M side of the triangle (center). As the reaction runs to completion, quartz and magnesite become incompatible and a new tie line forms between talc and dolomite (right). Note that dolomite does not participate in the reaction at all.
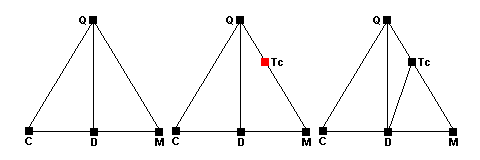
Around 450 C, dolomite ceases to coexist with quartz and the reaction
3Dol + 4Qz + H2O = Tc + 3Cal + 3CO2 occurs. The Q-D tie line disappears (center) and there are 4 phases present at equilibrium. As the reaction runs to completion a new tie line joining talc and calcite appears (red, right). Note that the dissolved tie line joins the reactants and the new tie line joins the products.
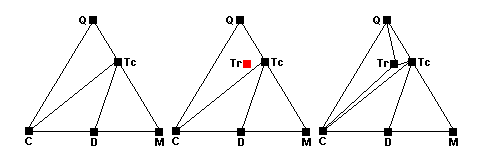
Around 500 C, quartz, calcite and talc react to form tremolite. The new tremolite point appears in the middle of the Q-Tc-C field (center) and as the reaction runs to completion, new tie lines joining tremolite with quartz, talc and calcite appear (right).
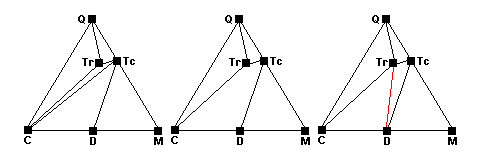
At slightly higher temperatures talc and calcite react. The talc-calcite tie line disappears and at equilibrium there are four phases present (center). As the reaction runs to completion a new tie line joining tremolite and and dolomite appear (red, right).
Return to Mineralogy-Petrology Index
Return to Thin-Section Index
Return to Crystals and Light Index
Return to Crystal Structures Index
Return to Mineral Identification Tables
Return to Professor Dutch's Home Page
Created 15 October 2009, Last Update
Not an official UW-Green Bay Site