Symmetry around a Point in the Plane
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, University of Wisconsin - Green Bay
Reflection and Rotation
Symmetry is the set of mathematical rules that describe the shape of an object. The two most common kinds are:
- Reflection or Mirror symmetry
- Rotation symmetry
Reflection or Mirror symmetry
Two halves of an object are mirror images of each other. The figures below have reflection symmetry.
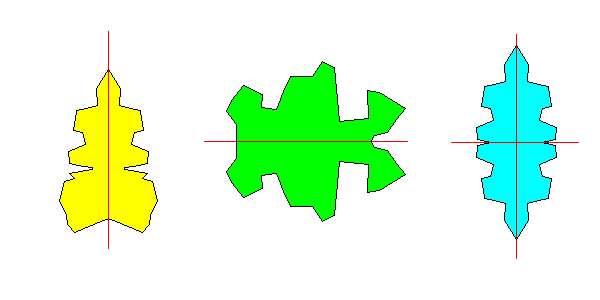
The letters A U V T Y all have reflection symmetry across a vertical plane. The letters D E C B have reflection symmetry across a horizontal plane. It is possible to have reflection symmetry in more than one direction, as in the object at right. The letters H I O X have both horizontal and vertical mirror symmetry. Note that:
- Objects can have more than one kind of symmetry.
- If they do, the symmetries have to be consistent. For example, you can't cross mirror planes at arbitrary angles.
- symmetry operations act on each other as well as on patterns. In the right-most figure above, note that each mirror plane is reflected by the other.
People and most vertebrates basically have mirror symmetry (at least externally). In biology it is often called bilateral symmetry.
A Trivia Question
When you look in a mirror, why are your left and right sides reversed, but not your top and bottom?
Rotational Symmetry
Parts of an object are related by rotation. As a general rule, you can rotate such an object through a certain angle and it will still have the same appearance.
The figures below have rotational symmetry:
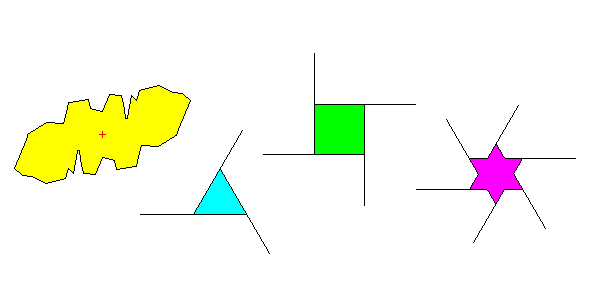
- In Figure a., the parts are related by a rotation around the center by 180 degrees. The figure looks the same twice in a 360-degree rotation. We say it has two-fold symmetry. The letters Z S and N also have two-fold symmetry.
- Figure b. looks the same three times during a 360-degree rotation and is said to have three-fold symmetry.
- Figure c. has four-fold symmetry and:
- d. has six-fold symmetry.
- An object is said to have n-fold symmetry if it looks the same after being rotated 360/n degrees.
- The point around which we rotate the object is called a symmetry axis.
Handedness (Chirality, Enantiomorphism)
Objects with rotational symmetry but no reflection symmetry exist in two forms that we might call "left-handed" and "right-handed". Objects with reflection symmetry are their own mirror image. Rotation symmetry without reflection is often used in graphic design to portray the idea of speed, power, or dynamic action.
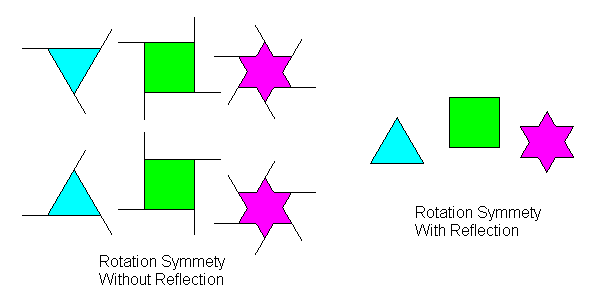
In chemistry, the fact that some molecules have left- and right- handed versions is called chirality from the Greek word for hand. The same root appears in the word "chiropractor." In crystallography, shapes that lack mirror symmetry are called enantiomorphic.
symmetry and the Real World
Real objects never are perfectly symmetrical. Even in a crystal, there are impurity atoms and defects that spoil the perfect symmetry. We say an object has symmetry if it does as a whole, apart from minor defects. For example, we say people have bilateral symmetry even though they may have a mole on one side of their face but not the other.
When symmetry becomes imperfect enough to be important depends on the situation. A ding in a boat propeller is less critical than a nick on a high-speed turbine blade.
One-fold symmetry = No symmetry
Some objects have no symmetry at all: a computer keyboard, a left glove, the letters G Q d p J L. In a 360 degree rotation, the object matches its original appearance only once, after a full 360 degrees. Thus, we can say the object has one-fold symmetry. One-fold symmetry is the same as no symmetry at all.
This might seem like a roundabout description but actually all the mathematical formulas for symmetry work equally well for this definition of one-fold symmetry. It allows us to develop formulas for all symmetries, even no symmetry at all.
symmetry within symmetry
Objects of high symmetry also contain lower symmetries as well. Hexagon abcdef below has six-fold symmetry. However, we can rotate it by 120 degrees and preserve its appearance, so it has 3-fold symmetry. We can rotate it by 180 degrees and preserve its appearance, so it also has 2-fold symmetry, and of course we can rotate it by 360 degrees and preserve its appearance, so it has one-fold symmetry as well. Everything has one-fold symmetry.
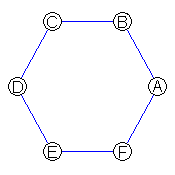
Thus, 6-fold symmetry automatically includes 3-, 2-, and 1-fold symmetry.
- a-b-c-d-e-f are related by six-fold symmetry
- a-c-e and b-d-f are related by three-fold symmetry
- a-d, b-e, c-f are related by two-fold symmetry.
In general, n-fold symmetry includes any lower number that divides n. An octagon has 8-, 4-, 2- and 1-fold symmetry.
Combining Symmetry Operations
Interesting things happen when we combine symmetries. For example, Figure a. below has reflection symmetry in two directions. However, it also has two-fold symmetry - it looks the same after a 180-degree rotation. The letters O H I X not only have mirror planes in two directions, but also two-fold symmetry as well.
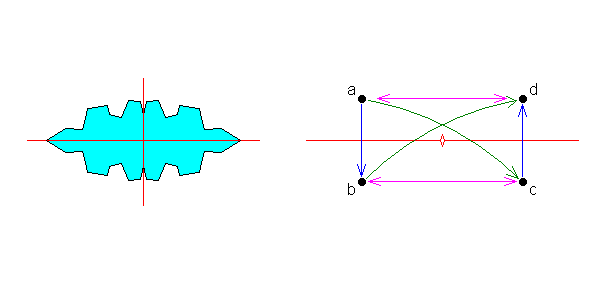
To see what happens, look at the figure on the right. In the mirror plane, point a is reflected to b. If we add a two-fold symmetry axis, point a is rotated to c and b is rotated to d. Note that c is a mirror image of d. Also note, though, that we can now draw a mirror plane at right angles to the original plane, and d is a mirror image of a, and c is a mirror image of b. Put two mirror planes at right angles, and you get a two-fold symmetry axis. Put a two-fold axis on a mirror plane, and you get a second mirror plane. We see three principles here:
- When you combine symmetries, often unexpected symmetries appear as well.
- When you combine symmetries, it doesn't matter in what order you combine the operations.
- When you combine symmetries, the operations have to yield consistent results (not all combinations do.)
When you combine other rotations with mirror planes, there may be many symmetries. Consider hexagon abcdef below:

- a-b-c-d-e-f are related by six-fold symmetry
- a-c-e and b-d-f are related by three-fold symmetry
- a-d, b-e, c-f are related by two-fold symmetry.
- a-f-e and b-c-d are related by mirror symmetry
- f-a-b and c-d-e are related by mirror symmetry
- a-b-c and d-e-f are related by mirror symmetry
- a-f and c-d are related by mirror symmetry across plane b-e
- a-b and d-e are related by mirror symmetry across plane c-f
- e-f and c-b are related by mirror symmetry across plane a-d
- Of course, a point on a mirror plane merely reflects onto itself.
Combining Rotation and Reflection
A hexagon illustrates that an interesting thing happens when we combine rotation and reflection. Consider the following two cases:
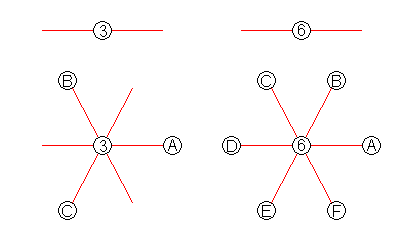
In the case of the three-fold axis, the rotation rotates the mirror plane from a to b and then to c. symmetry operations act not only on patterns, but on other symmetry operations. The six-fold rotation rotates the mirror plane to b, c, d, e, and f, but a-d, b-e and c-f are the same: flipping a mirror plane 180 degrees merely flips it over onto itself. At first glance, the two situations look alike. So let's take a second glance.
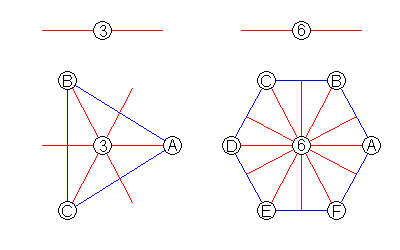
In the case of a three-fold axis and a mirror plane, only three planes of symmetry result. But when a six-fold axis is involved, we get not only three mirror planes by direct rotation, but three unexpected ones as well. symmetry that is created by the interactions of other symmetries is called induced.
- When we combine a mirror plane with an odd-fold axis of rotation, we get only the mirror planes created by rotation.
- When we combine a mirror plane with an even-fold axis of rotation, we get the mirror planes created by rotation, plus another set halfway between them.
- In either case, when a mirror-plane is combined with an n-fold axis of rotation, there are n distinct mirror planes separated by 180/n degrees.
When n is odd, every rotation results in a new mirror plane, because the rotated left end of each plane falls between the right ends of two others. But every even-fold rotation results in a 180 degree rotation that simply flips the mirror planes over onto themselves, so that half the mirror planes are duplicates of each other. It's almost as if nature creates a second set to compensate.
Notation
We're now ready to set up some notation for symmetry operations:
- Simple rotation symmetry is simply described by a number: three-fold rotation is simply described as 3. A swastika has symmetry 4.
- Mirror planes are described by m.
- Compound symmetries are described by joining symbols. Odd-fold rotation plus reflection, like that of a triangle, is 3m. The stars on an American flag have symmetry 5m.
- When the rotation is even-fold, we also note the second set of mirror planes that is created. A rhombus has symmetry 2mm, a square has 4mm, a hexagon or star of David has 6mm.
- All regular polygons have symmetry nm if n is odd or nmm if n is even.
o
/ \ / \
o---o o---o
\ \ / /
o---o---o
/ / \ \
o---o o---o
\ /
o
Answer to Trivia Question:
A mirror doesn't reverse right and left: it reverses front and back. The mirror plane is perpendicular to your line of sight. The left side of your image is on your left side, and the right side of your image is on your right side. We only think the mirror reverses right and left because we'd have to turn around to face the way our image faces.
Return to symmetry Index
Return to Crustal Materials Index
Return to Professor Dutch's home page
Created 11 Feb. 1997, Last Update Sept. 22, 1999