Aperiodic Tilings
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, University of Wisconsin - Green Bay
It's easy to construct tilings that are aperiodic. Radial and spiral tilings are aperiodic, for example. The challenge is to find tilings that are only aperiodic. Not only must the polygons tile the plane non-periodically, but no subset may tile periodically. One can easily devise a tiling with a single pentagon surrounded by triangles. While the complete set of tiles is aperiodic, the triangles can tile the plane periodically, so this example is not a valid aperiodic tiling.
Depiction of Tilings
All known aperiodic tilings are based on shapes that can also tile the plane periodically. In order to force aperiodic tiling, we have to modify the tiles in various ways:
- Notches and Tabs: An obvious method of forcing tiles to go together in certain ways is to put notches and tabs of various shapes along the edges. The Robinson Tiles shown below use this approach.
- Key Tiles: Tiles can also be forced to fit in certain ways by creating key tiles that fit mating notches on adjacent tiles. Key tiles allow more versatility in matching tiles than notches and tabs. The Ammann Tiling shown below under Composition uses this approach.
- Patterned Tiles: In many cases the tiles create highly symmetrical patterns that would be masked by tabs or key tiles. In such cases, patterns can be drawn on the tiles, with the rule that patterns must match across tile edges. This approach is commonly used with Penrose Tilings. A variation on this technique is Ammann Bars, lines that continue straight across tile edges.
Robinson Tilings
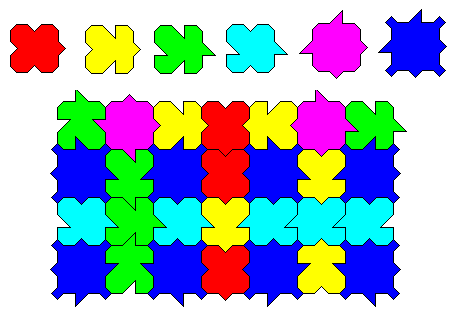 |
For a long time it was believed that all sets of tiles that covered the plane must tile periodically, but in 1964 Robert Berger found a set of tiles that do not. In 1976 Raphael Robinson simplified the set to six. The tiles are based on work done by Hao Wang in 1961, which originally involved tiling the plane with squares having different-colored edges. Such tiles are called Wang dominoes. |
 |
In the example at left we see how attempts to tile periodically with Robinson Tiles break down. We start with a completely uniform row, manage to maintain periodicity in the next three rows, but then periodicity breaks down in the last row. In the third row we started tiling with the green tiles. |
Suppose we'd continued the vertical row of red tiles? The only tile that would fit adjacent to a red tile would be another red one on either side. Then we'd need a yellow tile beneath the green ones. A red tile would fit again in the lower left corner, so the fifth row would be RYRRRYxxxx. So far, so good. We can fit a red tile to the right of the second yellow tile, but then what? We have a space flanked above and to the left by red tiles, both with dimples. The only tile with two bumps of the proper shape is a purple tile. The periodicity still breaks down.
Ammann Tilings
 |
Robert Ammann discovered a number of aperiodic tilings, which are described in Grunbaum and Shephard's Tilings and Patterns. They are all quite different and are called Ammann Tilings solely to denote their authorship. |
Kepler Tilings
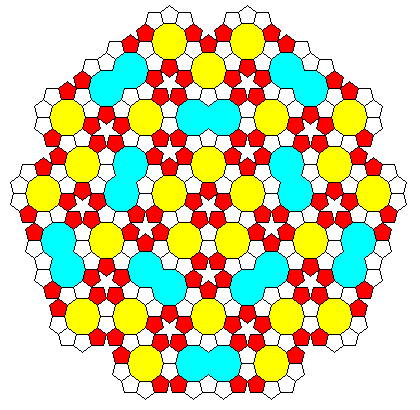 |
Some of the first modern work on tilings was done by Johannes Kepler. He also was one of the first mathematicians to treat star polygons as regular polygons. This tiling is based on one of Kepler's figures. None of the component polygons tile the plane periodically. Is this a true aperiodic tiling? |
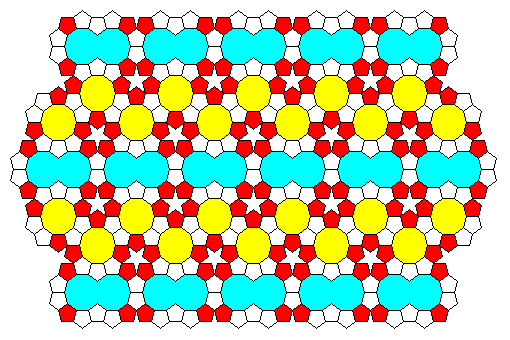 |
No, it isn't. Although none of the individual polygons tile the plane periodically, the entire set does. Nevertheless, Penrose Tilings (below) were inspired by Kepler's Tilings. |
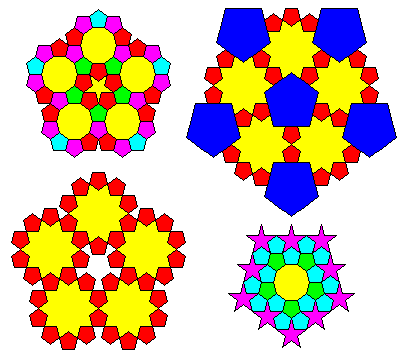 |
Kepler also discovered a number of ways pentagons and related polygons can cover portions of the plane. |
Penrose Tiles
 |
In 1974, Roger Penrose discovered an aperiodic tiling that uses only two shapes, nicknamed kites and darts. They can be prevented from tiling periodically by putting notches and tabs on the edges of the tiles, but a more aesthetic approach is to color the tiles as shown and require the edges to match. |
Long-Range Order in Aperiodic Tilings
Composition
Although aperiodic tilings are not periodic, all known examples have profound long-range order. Most of them permit composition, in which tiles can be combined to make larger replicas of themselves. Since tiles can always be combined into larger replicas, composition is a basic method of proving that an aperiodic tiling can cover an infinite plane.
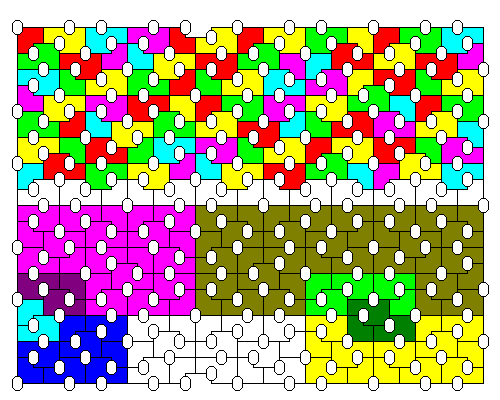 |
In the Ammann tiling at left, there are two shapes of tiles (plus a third key tile). In the lower half of the diagram, tiles are colored to show how higher-order replicas can be built. The stubby tile is colored in shades of blue and purple, the elongate tile in shades of yellow and green. In the upper half, first-order tiles are colored so that second-order tiles are formed by blue and purple pieces or red, yellow and green pieces. |
Ammann Bars
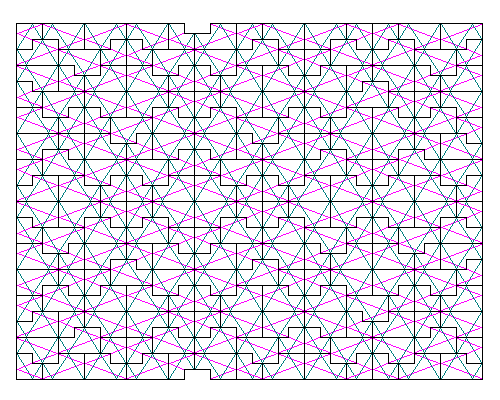 |
Aperiodic tilings are one thing. It's not too surprising that we can color aperiodic tiles and discover symmetries. But it is surprising indeed that we can place straight lines on the tiles in such a way that the lines continue across the whole pattern. Such lines are called Ammann Bars. This is one of Ammann's tilings with bars shown in color. The tile edges also align to form straight lines, but sooner or later there is some interruption to the pattern. Nevertheless, the Ammann bars continue across the entire tiling. |
Hierarchy
 |
Most aperiodic tilings have some kind of heirarchical structure. Composition is one variety. This Ammann Tiling shows another. The asymmetrical notches force tiles to align in certain directions as shown by the dark purple lines. These lines generate a hierarchy of progressively larger H-shaped patterns. Each H is mirror-symmetrical, but the join to the next level H prevents any long-range periodicity. |
References
Martin Gardner, Extraordinary nonperiodic tiling that enriches the theory of tiles, Mathematical Games, Scientific American, January, 1977, p. 110-121
Grunbaum, B and Shephard, G. C., Tilings and Patterns, Freeman, 1987. Just about everything there was to know on the subject at the time.
Return to Symmetry Index
Return to Professor Dutch's Home Page
Created 1 August 1999, Last Update 29 May 2003