Archimedean polyhedra
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, University of Wisconsin - Green Bay
The Archimedean polyhedra are polyhedra with regular polygon faces. Faces may be of different types but all the vertices are identical. There are thirteen of then, shown below.
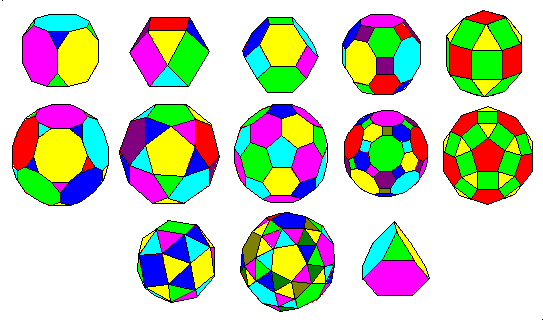
Except for the truncated tetrahedron, lower right, all the Archimedean polyhedra are modifications of the cube-octahedron pair or the dodecahedron-icosahedron pair. The above figure groups the polyhedra according to their geometric similarities.
- Top Row:
- Truncated Cube
- Cuboctahedron
- Truncated Octahedron
- Great Rhombicuboctahedron
- Lesser Rhombicuboctahedron
- Second Row:
- Truncated Dodecahedron
- Icosidodecahedron
- Truncated Icosahedron
- Great Rhombicosidodecahedron
- Lesser Rhombicosidodecahedron
- Third Row:
- Snub Cube
- Snub Dodecahedron
- Truncated Tetrahedron
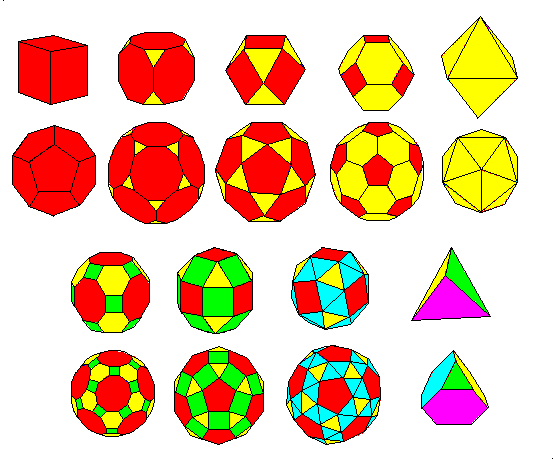
The top two rows in the figure above shows how the Archimedean polyhedra can be obtained by modifying the Platonic solids. Progressive truncation of a cube can lead ultimately to an octahedron and vice-versa. Likewise.progressive truncation of a dodecahedron can lead ultimately to an icosahedron and vice-versa.
In the bottom two rows, additional faces are added between the faces of a cuboctahedron or icosidodecahedron, with appropriate modifications of polygon shape. The tetrahedron and truncated tetrahedron are shown in the last pair. Further truncation of the tetrahedron would eventually lead to eight triangular faces, an octahedron.
Archimedean polyhedra and Tilings
Archimedean polyhedra and Archimedean tilings are closely related as shown below. In each case n denotes an integer. For example, in the top row we see a truncated tetrahedron with vertices 3.6.6 (n=3), a truncated cube with 3.8.8 (n=4), a truncated dodecahedron with 3.10.10 (n=5). When n = 6, the polygon angles sum to 180 degrees and we obtain the 3.12.12 tiling. All the other families are similarly arranged with n ranging from 3 to 6.
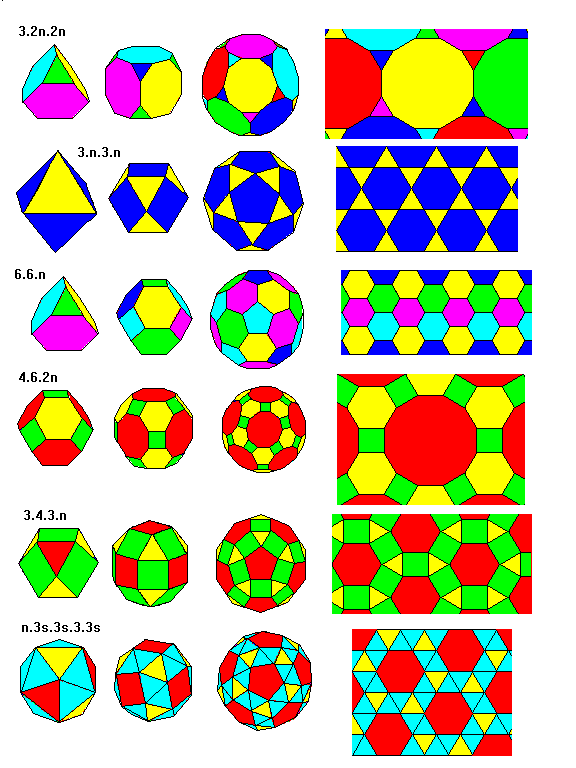
Snub polyhedra have triangular faces not created by a threefold symmetry axis. In each case in the last row the threefold axis face is colored differently from the extra or snub faces. The vertex description denotes snub faces with s. If we attempt to construct a snub tetrahedron, we have four triangular tetrahedron faces, four triangular faces at the threefold symmetry axes, and pairs of triangles at each of the six tetrahedron edges, a total of 4 + 4 + 2*6 = 20. A solid with 20 equilateral triangle faces is an icosahedron. Thus, a snub tetrahedron is an icosahedron. An icosahedron colored to show this relationship is shown.
Return to Symmetry Index
Return to Professor Dutch's Home page
Created 2 Oct. 1997, Last Update 2 Oct. 1997