Best Representations of 3-Dimensional Symmetry: Minimal Faces

Steven Dutch, Professor Emeritus, Natural and Applied Sciences, University of Wisconsin - Green Bay

What Do We Mean By "Best?"

I was first inspired to consider this problem while building a set of solids to represent all 32 crystal classes (most commercial model sets omit the less common and less symmetrical classes). I soon realized the answers were different depending on whether I was cutting models out of wood or building them out of cardboard, and whether I was thinking of ease of construction or aesthetic appeal.

Some reasonable possible definitions of "best" include:

Triclinic

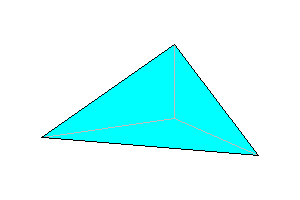1

General tetrahedron. It is a remarkable fact that fully eight of the 32 crystal classes can be represented by tetrahedra.

4 faces
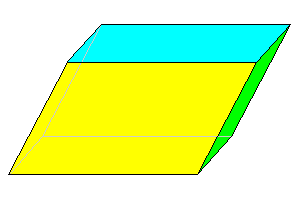1*

General oblique parallelepiped

6 faces

Monoclinic

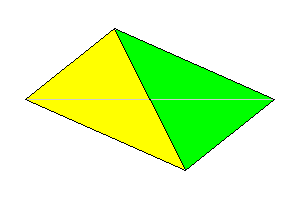2

Tetrahedron with 2-fold axis

4 faces
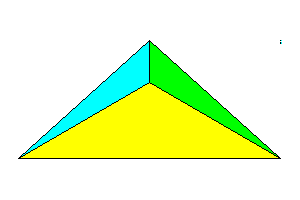m

Tetrahedron with mirror plane

4 faces
2/m

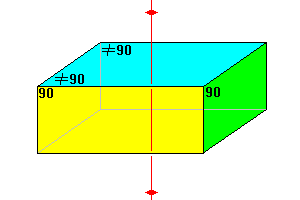
General monoclinic prism

6 faces

Orthorhombic

222

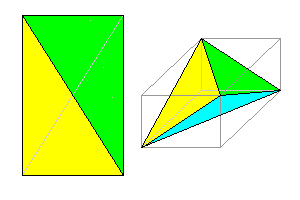
Orthorhombic disphenoid

4 faces. Also isohedral
mm

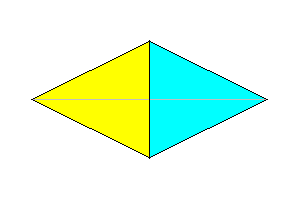
Tetrahedron with two mirror planes

4 faces
2/m 2/m 2/m

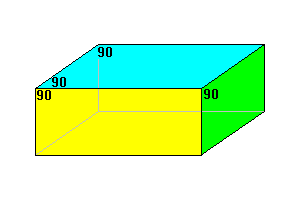
General rectangular parallelepiped

6 faces

Uniaxial Classes

The uniaxial classes which have a single major symmetry axis and additional twofold axes or mirror planes all have certain features in common. For each group, whether trigonal, tetragonal or hexagonal, there are seven possible classes (but some turn out to be degenerate). These can all be derived by taking one of the seven strip space groups and wrapping it around a cylinder. If N is the degree of symmetry, we have:

N
A single major symmetry axis alone. Requires an additional N faces arbitrarily oriented to the first set to break up any mirror symmetries. We can combine two dissimilar pyramids rotated with respect to each other, for a total of 2N faces.
N/m
Symmetry axis perpendicular to a mirror plane. An N-fold dipyramid (2N faces) plus an N-fold prism at an arbitrary angle to the pyramid will produce this symmetry. 3N faces required.
Nm
Symmetry axis with mirror planes intersecting along the axis. N-sided pyramids have this symmetry, requiring N+1 faces.
N/m m
Symmetry axis perpendicular to a mirror plane, and mirror planes intersecting along the axis. A combination of N/m and Nm. This is the holosymmetric class: it contains all the other symmetries as subsets. N-sided prisms have this symmetry, requiring N+2 faces.
N2
Symmetry axis with 2-fold axes perpendicular to it. A general trapezohedron with no mirror planes has this symmetry and is also isohedral. 2N faces.
N*
N-fold rotoinversion axis. Rotoinversion is complex. For N odd we have a mirror-symmetric trapezohedron with 2N faces plus a skew set of 2N prism faces to break up the symmetry, for a total of 4N faces.
N*2m
N-fold rotoinversion axis with 2-fold axes perpendicular to it and with mirror planes intersecting along the N-fold axis. For N odd we have a mirror-symmetric trapezohedron with 2N faces 

Trigonal - Rhombohedral

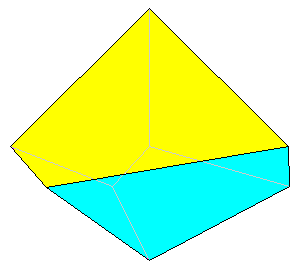3

Two skew dissimilar pyramids

6 faces. 
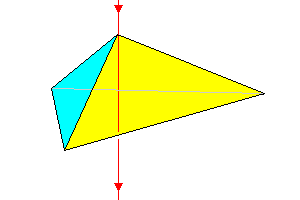3m

Trigonal pyramid with flat base

4 faces
(Same as 6*) 3/m 
(Same as 6* 2/m) 3/m m 
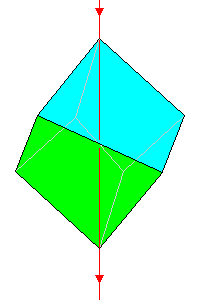32

Trigonal trapezohedron

6 faces. Also isohedral
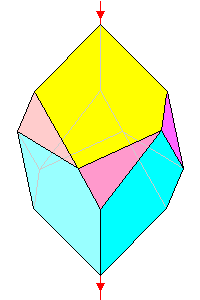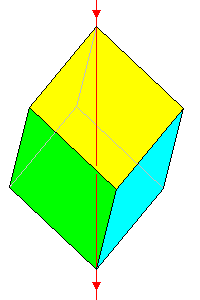
3*

Trapezohedron with skew prism faces

12 faces
3*2m

Rhombohedron. Also isohedral and equilateral.

6 faces.

Tetragonal 

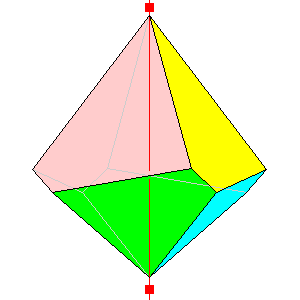4

Two skew dissimilar pyramids

8 faces. 
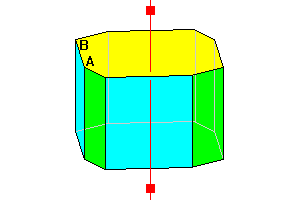4/m

Tetragonal prism with second set of skew faces. Angle A not equal to B and sets of faces not congruent.

10 faces
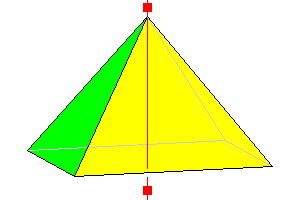4mm

Tetragonal pyramid

5 faces
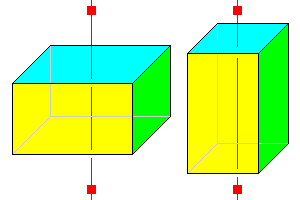4/m 2/m 2/m

Square prism

6 faces
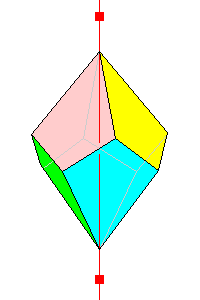422

Tetragonal trapezohedron

8 faces. Also isohedral
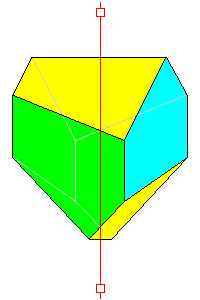4*

Skew truncated prism

8 faces
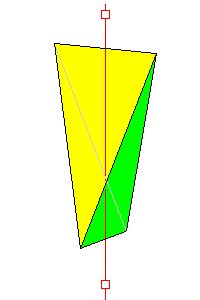4* 2/m

Tetragonal disphenoid

4 faces. Also isohedral

Hexagonal 

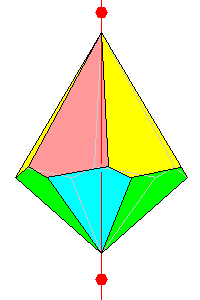6

Two skew dissimilar pyramids

12 faces. 
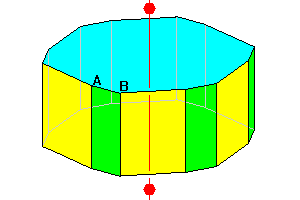6/m

Hexagonal prism with second set of skew faces. Angle A not equal to B and sets of faces not congruent.

14 faces
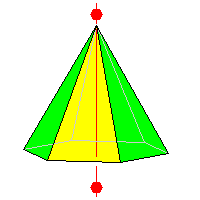6mm

Hexagonal pyramid

7 faces
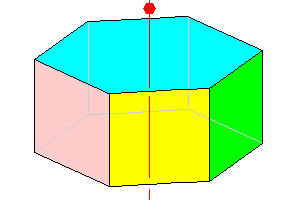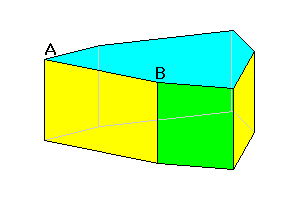
6/m 2/m 2/m

Hexagonal prism

8 faces. 
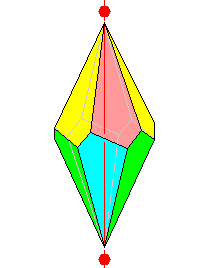622

Hexagonal trapezohedron

12 faces. Also isohedral
6* (same as 3/m)

Triangular prism with second set of skew faces. Angle A not equal to B and sets of faces not congruent.

8 faces
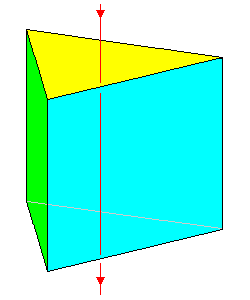6* 2/m

Trigonal prism. Also equilateral and regular-faced.

5 faces

Isometric

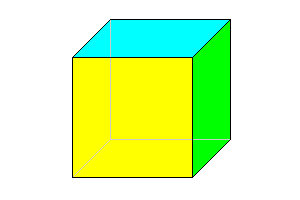4/m 3* 2/m

Cube. Also isohedral, equilateral and regular-faced

6 faces
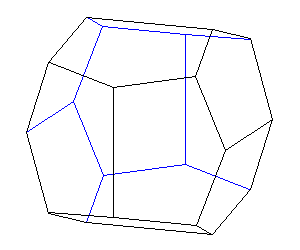2/m 3*

Non-regular pentagonal dodecahedron (pyritohedron)

12 faces
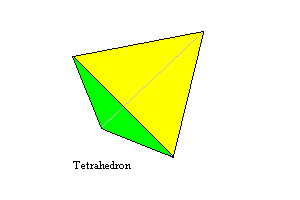4* 3m

Tetrahedron. Also isohedral, equilateral and regular-faced.

4 faces
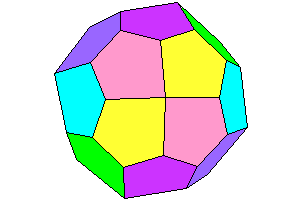432

Gyroid. Also isohedral.

24 faces
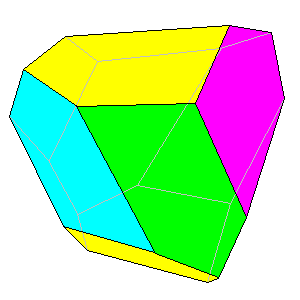23

Tetartoid. Also isohedral.

12 faces

Return to Symmetry Index
Return to Professor Dutch's Home page

Created 31 July 2001, Last Update 10 June 2020