Bravais Lattices
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, University of Wisconsin - Green Bay
In two dimensions, periodic unit cells can have one of five basic shapes: general parallelogram, general rectangle, square, 60-120 degree rhombus, and generic rhombus. The last is often described as a "centered" lattice, a rectangle with an extra point in the middle, to bring out the rectangular nature of the pattern.
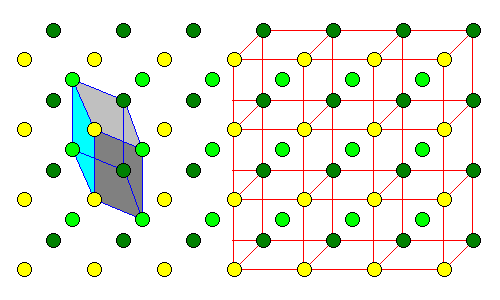 |
It's not too hard to see the rectangular pattern in a rhombic lattice, but it can be very hard to see the patterns in three dimensional lattices. At left, for example, is a cubic lattice with an extra point in the center, a so-called body-centered lattice. At far left is the simplest cell shape, but the cubic nature of the lattice is totally impossible to see. |
For this reason, three-dimensional lattices must often be described as unit cells with additional points. There are 14 basic unit cells in three dimensions, called the Bravais Lattices.
Symbols
- P - Primitive: simple unit cell
- F - Face-centered: additional point in the center of each face
- I - Body-centered: additional point in the center of the cell
- C - Centered: additional point in the center of each end
- R - Rhombohedral: Hexagonal class only
Isometric Cells
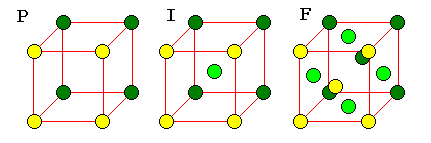 |
| The F cell is very important because it is the pattern for cubic closest packing. There is no C cell because such a cell would not have cubic symmetry. |
Tetragonal Cells
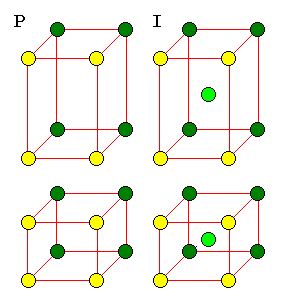 |
| A C cell would simply be a P cell with a smaller cross-section, as shown below. An F cell would reduce to a network of I cells. |
 |
Hexagonal Cells
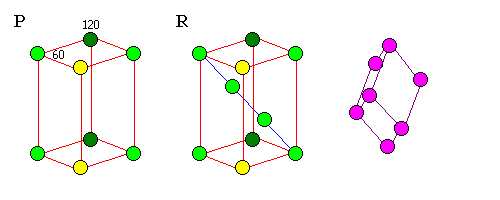 |
| The R cell is unique to hexagonal crystals. The two interior points divide the long diagonal of the cell in thirds. This is the only Bravais lattice with more than one interior point. A rhombohedron can be thought of as a cube distorted along one of its diagonals. More information on the rhombohedral lattice. |
Orthorhombic Cells
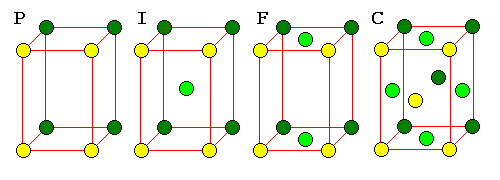 |
| The orthorhombic class is the only one with all four types of Bravais lattice |
Monoclinic and Triclinic Cells
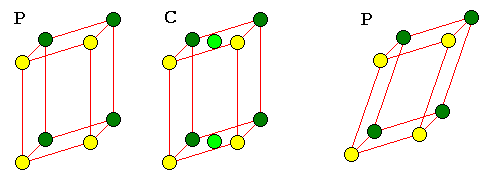 |
| Monoclinic F or I cells could also be represented as C cells. Any other triclinic cell can also be represented as a P cell. |
Return to Symmetry Index
Return to Crustal Materials (Mineralogy-Petrology) Index
Go to Recreational Mathematics Index
Return to Professor Dutch's Home Page
Created 13 Oct 1997, Last Update 13 Oct 1997