Rep-Tiles
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, University of Wisconsin - Green Bay
Rep-tiles, or Replicating Tiles, are tiles that can be joined together to make larger replicas of themselves. The term "rep-tile" was coined by mathematician Solomon Golomb, a prolific contributor to geometrical recreations of all sorts.
Rep-tiles that require n tiles to build a larger version of themselves are said to be rep-n. For example, we can combine four squares to make a bigger square, so a square is rep-4. Since we can combine any of those replicas into a second-generation copy, a rep-n tile is also rep-n2, rep-n3, and so on. Often tiles have several rep-numbers. If a tile is rep-n and rep-m, it is also rep-mn, since we can build replicas with n tiles, then combine m of those into a yet larger version. Obviously, everything is also (trivially) rep-1.
All Triangles and Parallelograms are Rep-Tiles
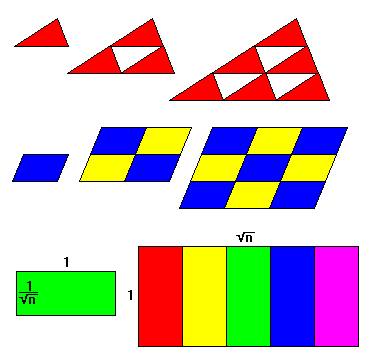 |
All triangles and parallelograms are rep-k2, where k is some integer.
Rep-k parallelograms for any value of k are easy to construct; they have edges of 1 and 1/sqrt(k). They need not be rectangles. |
Some Special Rep- Triangles
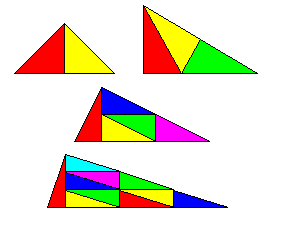 |
|
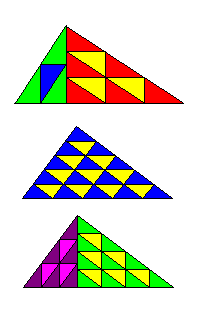 |
|
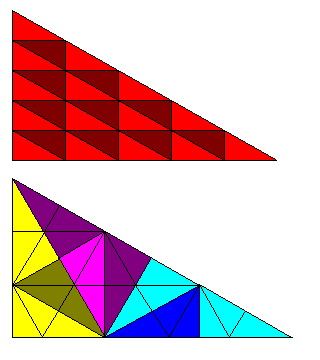 |
The 30-60-90 triangle is both rep-25 (52) and rep-27 (33, by combining three generations of rep-3 triangles). |
Fractal tilings
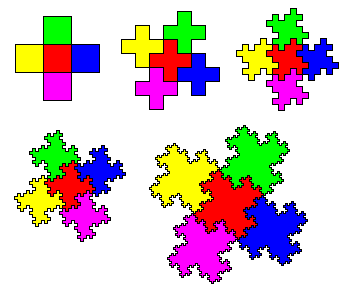 |
Four squares can be arranged around a central square to form a Greek Cross. Greek Crosses make a lovely plane tesselation, but they are not rep-tiles. We can try modifying a Greek Cross tesselation by replacing each cross with the compound of five crosses. It's closer, but still not an exact rep-tile. We can repeat the process, each time getting figures that are more and more crinkled and closer to a true rep-tiling. But at every step, we see that the perimeter of the tiling always has twice as many crinkles as each tile. |
If we continue the process to infinity, however, then the tiles would have infinitely crinkly edges and would tesselate to make a true rep-5 tiling. The compound of five figures would be a scaled-up exact replica of each tile. Amazingly, the perimeter of each tile is infinite, even though the area of the tiles is obviously finite. A weird figure of this sort, whose perimeter behaves as if it's not merely one-dimensional, but not quite two-dimensional either, is called a fractal. The fact that the compound of five tiles is a bigger, but still exact, replica of the individual tiles, is called self-similarity. Since tiling deals with similar figures, and many fractals are self-similar, it should be no surprise that many fractals are rep-tiles.
Obviously, since neither computers nor human draftsmen can generate curves that are infinitely long and infinitely crinkly, nobody has ever drawn a true fractal. Since no physical system that we know of is infinite, nobody has ever seen a real fractal either. True fractals are ideal concepts that are only approximately achieved in physical reality - Plato would have been enthralled by them. Most fractals are approximately represented as in the last figure above, with detail close to the resolution limit of the picture but not quite, so that the fine structure is still visible.
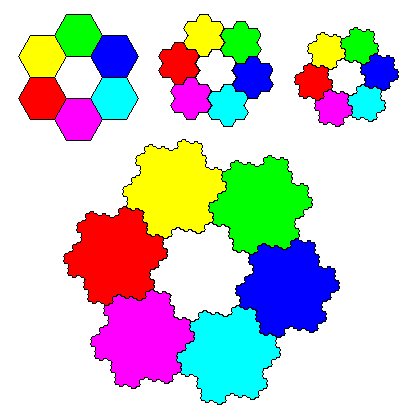 |
At left is another example. Hexagons cannot be arranged to form a rep-tile, but the cluster of six around a central seventh hexagon comes close. If we replace each hexagon with a compound of seven, we get closer yet, and after an infinite number of cycles we achieve a true rep-7 fractal. |
Return to Symmetry Index
Return to Professor Dutch's home page
Created July 9, 1999, Last Update July 9, 1999
Not an official UW-Green Bay site