Stellations of polyhedra
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, University of Wisconsin - Green Bay
Stellation
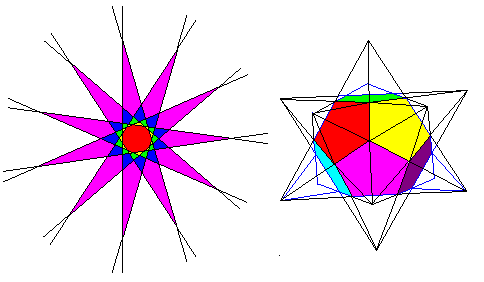
If you extend the edges of a polygon, they intersect to form a star. In the left diagram above, an 11-sided polygon has its edges extended to form star polygons. Each possible star is denoted by a different color. Beyond the outermost star, all the lines diverge, and never intersect again. Likewise, we can extend the faces and edges of a polyhedron. If we do this to a dodecahedron, as shown at right, the faces become stars and we obtain the star polyhedron shown. This process is called stellation
Stellations of Simple polyhedra
Below are shown stellations of the tetrahedron, cube, octahedron, pentagonal dodecahedron and rhombic dodecahedron. Stellations of the icosahedron are much more complex and shown on separate pages.
Tetrahedron and Cube
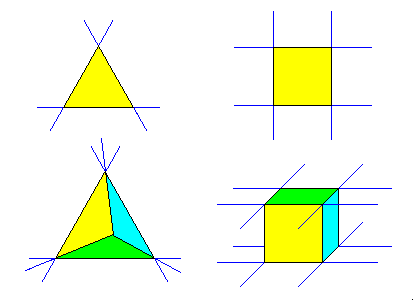 |
The edges of a cube or tetrahedron, once extended, never meet. These solids have no stellations. |
Octahedron
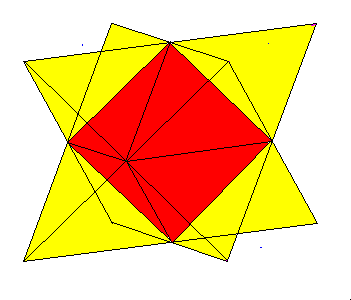 |
The only stellation of the octahedron is Kepler's Stella Octangula, which is also a compound of two tetrahedra. |
Pentagonal Dodecahedron
 |
Here we see a dodecahedron face (blue) with the intersections of all other faces indicated. This is a common way to show the possible stellations of a solid. We see that there are three distinct groups of cells. |
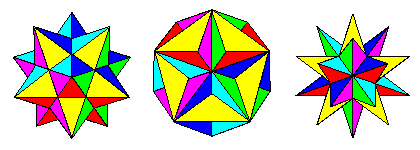
The three stellations of the dodecahedron are shown here. The first or innermost is the small stellated dodecahedron, discovered by Kepler. Next is the great dodecahedron, discovered by Poinsot in 1809. This is obtained by continuing the star planes of the small stellated dodecahedron outward until they meet to form the next set of pentagons. If we extend these pentagons, we get the stellation on the right, the great stellated dodecahedron, also discovered by Kepler.
Rhombic Dodecahedron
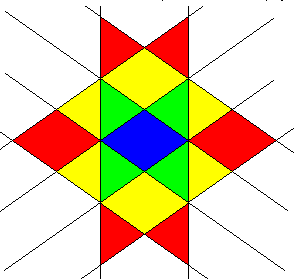 |
Here one face of a rhombic dodecahedron (blue) is shown with its edge extensions and the intersections of all the other faces. The different layers of cells formed by stellation are shown in color. |
 |
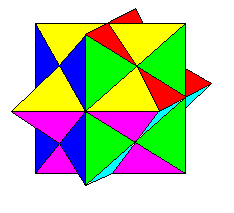 |
Left: the rhombic dodecahedron
Right: first stellation of the rhombic dodecahedron |
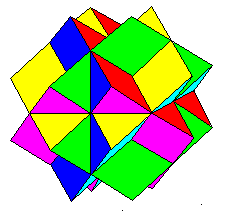 |
 |
Left: second stellation of the rhombic dodecahedron
Right: third and final stellation of the rhombic dodecahedron |
Return to Symmetry Index
Return to Professor Dutch's Home page
Created 16 February 1998, Last Update 16 February 1998