Stewart Toroids
(Toroidal Solids with Regular polygon Faces)
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, University of Wisconsin - Green Bay
The late Professor Bonnie Stewart became interested in the existence of toroidal solids (solids with holes) that also had regular polygon faces. He published his findings in a lovely but hard-to-find book - it was privately published - called Adventures Among the Toroids. My one complaint is that it was hand-lettered in a very attractive but hard to read calligraphy.
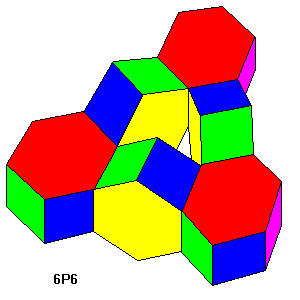 |
One of Stewart's first discoveries was the ring of hexagonal prisms shown here. |
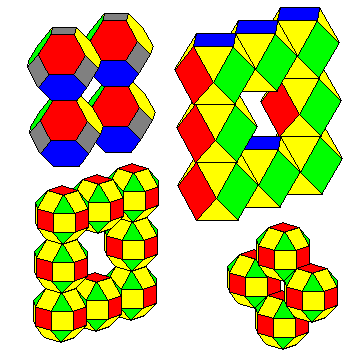 |
It is possible to combine various cubic polyhedra to make an infinite number of toroidal shapes as shown here. Often these can be continued indefinitely and form what might be termed "hyperbolic" tesselations. |
 |
Other solids, like octahedra, can also be joined to form rings. |
 |
Icosahedra can be inscribed within the octahedron, so icosahedra can also be joined in a similar way to make a ring. |
Notation and Definitions
Once a toroidal polyhedron has been found, we can derive an infinite number of others by tacking polyhedra onto free faces. Most of these are trivial.
To eliminate trivial cases, Stewart concentrated on polyhedra that were aplanar, that is, adjacent pairs of faces were not coplanar. He also concentrated on polyhedra that were quasi-convex, that is, were derived by tunneling into a convex polyhedron.
Since all the Stewart toroids have regular faces, they have a close connection with the Johnson Solids, the convex solids with regular polygon faces. Stewart's notation was a modification of Johnson's, of the form xxx/yyy, where xxx is the notation for the enclosing polyhedron and yyy is the notation for the portion excavated.
The genus of a toroid, loosely speaking, is the number of holes in it.
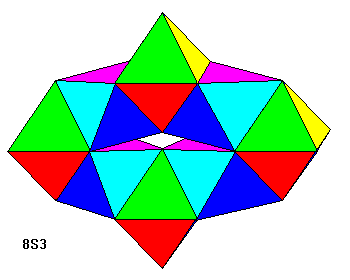
Apart from rings whose toroidal properties are obvious, most of the toroid illustrations consist of two parts: the left image is of the hole and the right image is the enclosing solid.
Families of Stewart Toroids
Variations on Truncated Cube
Variations on Pentagonal Rotunda
Variations on Triangular Cupola
Other Simple Genus 1 Solids
Go to Symmetry Index
Go to Recreational Mathematics Index
Return to Professor Dutch's Home Page
Created 1 March 1999, Last Update 1 March 1999