The 48 Special Crystal Forms
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, University of Wisconsin - Green Bay
Forms, Open and Closed
Any group of crystal faces related by the same symmetry is called a form. There are 47 or 48 crystal forms depending on the classification used.
Closed forms are those groups of faces all related by symmetry that completely enclose a volume of space. It is possible for a crystal to have faces entirely of one closed form. Open forms are those groups of faces all related by symmetry that do not completely enclose a volume of space. A crystal with open form faces requires additional faces as well. There are 17 or 18 open forms and 30 closed forms.
Triclinic, Monoclinic and Orthorhombic Forms
- Pedion
- A single face unrelated to any other by symmetry. Open
- Pinacoid
- A pair of parallel faces related by mirror plane or twofold symmetry axis. Open
- Dihedron
- A pair of intersecting faces related by mirror plane or twofold symmetry axis. Some crystallographers distinguish between domes (pairs of intersecting faces related by mirror plane) and sphenoids (pairs of intersecting faces related by twofold symmetry axis). All are open forms
- Pyramid
- A set of faces related by symmetry and meeting at a common point. Open form.
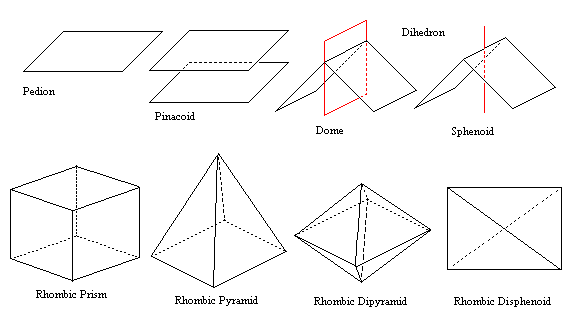
3-, 4- and 6-Fold Prisms
- Prism
- A collection of faces all parallel to a symmetry axis. All are open.
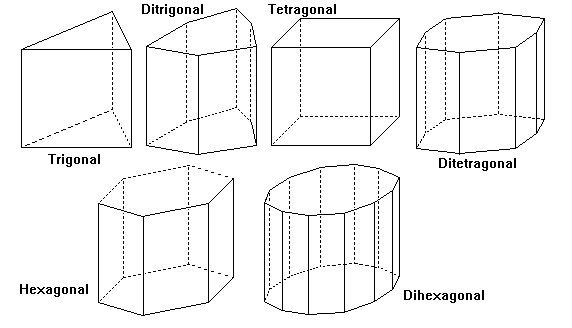
3-, 4- and 6-Fold Pyramids
- Pyramid
- A group of faces intersecting at a symmetry axis. All are open. The base of the pyramid would be a pedion.
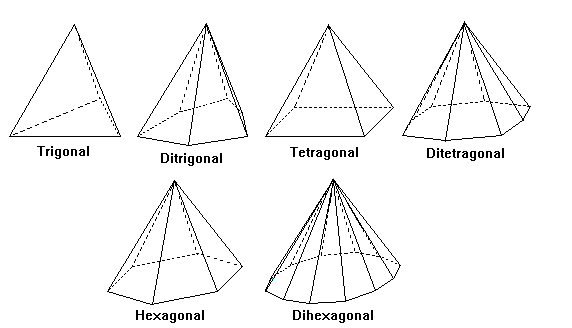
3-, 4- and 6-Fold Dipyramids
- Dipyramid
- Two pyramids joined base to base along a mirror plane. All are closed, as are all following forms.
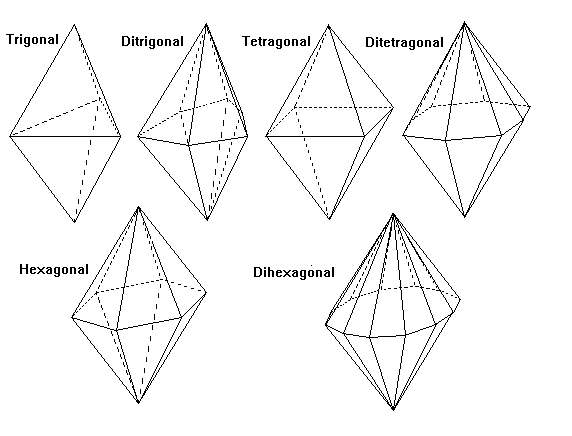
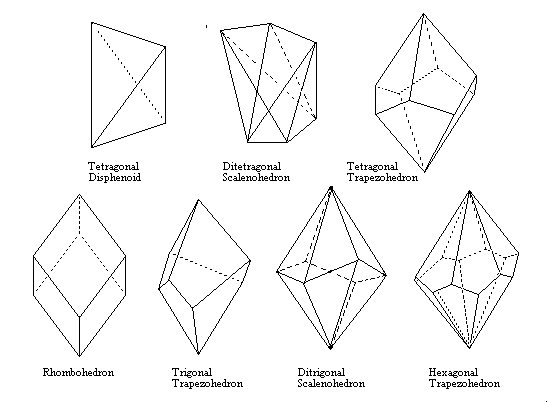
Scalenohedra and Trapezohedra
- Disphenoid
- A solid with four congruent triangle faces, like a distorted tetrahedron. Midpoints of edges are twofold symmetry axes. In the tetragonal disphenoid the faces are isoceles triangles and a fourfold inversion axis joins the midpoints of the bases of the isoceles triangles.
- Scalenohedron
- A solid made up of scalene triangle faces (all sides unequal)
- Trapezohedron
- A solid made of trapezia (irregular quadrilaterals)
- Rhombohedron
- A solid with six congruent parallelogram faces. Can be considered a cube distorted along one of its diagonal three-fold symmetry axes.
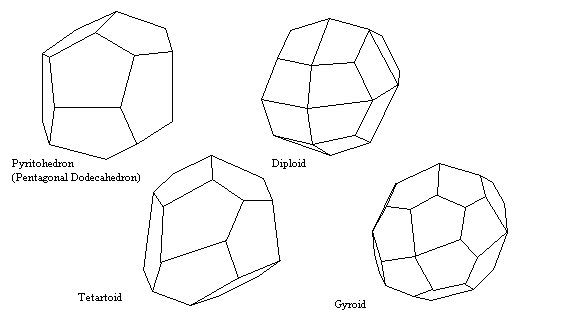
Tetartoidal, Gyroidal and Diploidal Forms
- Tetartoid
- The general form for symmetry class 233. 12 congruent irregular pentagonal faces. The name comes from a Greek root for one-fourth because only a quarter of the 48 faces for full isometric symmetry are present.
- Gyroid
- The general form for symmetry class 432. 24 congruent irregular pentagonal faces.
- Diploid
- The general form for symmetry class 2/m3*. 24 congruent irregular quadrilateral faces. The name comes from a Latin root for half, because half of the 48 faces for full isometric symmetry are present.
- Pyritohedron
- Special form (hk0) of symmetry class 2/m3*. Faces are each perpendicular to a mirror plane, reducing the number of faces to 12 pentagonal faces. Although this superficially looks like the Platonic solid with 12 regular pentagon faces, these faces are not regular.
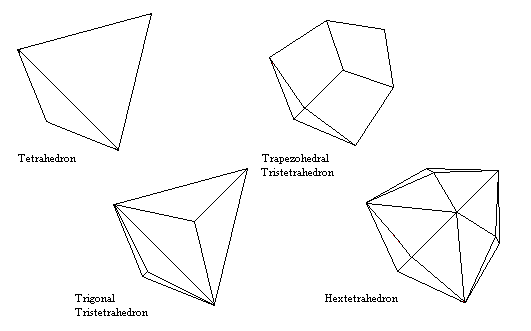
Hextetrahedral Forms
- Tetrahedron
- Four equilateral triangle faces (111)
- Trapezohedral Tristetrahedron
- 12 kite-shaped faces (hll)
- Trigonal Tristetrahedron
- 12 isoceles triangle faces (hhl). Like an tetrahedron with a low triangular pyramid built on each face.
- Hextetrahedron
- 24 triangular faces (hkl) The general form.
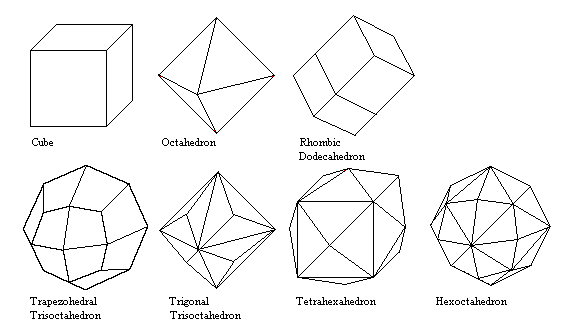
Hexoctahedral Forms
- Cube
- Six square faces (100).
- Octahedron
- Eight equilateral triangle faces (111)
- Rhombic Dodecahedron
- 12 rhombic faces (110)
- Trapezohedral Trisoctahedron
- 24 kite-shaped faces (hhl). Note that the Miller indices for the two trisoctahedra are the opposite of those for the tristetrahedra.
- Trigonal Trisoctahedron
- 24 isoceles triangle faces (hll). Like an octahedron with a low triangular pyramid built on each face.
- Tetrahexahedron
- 24 isoceles triangle faces (h0l). Like an cube with a low pyramid built on each face.
- Hexoctahedron
- 48 triangular faces (hkl) The general form
Return to Symmetry Index
Return to Crustal Materials (Mineralogy-Petrology) Index
Return to Recreational Mathematics Index
Return to Professor Dutch's Home Page
Created 15 Sep 1997, Last Update 31 May 2020