Uniform polyhedra
Steven Dutch, Professor Emeritus, Natural and Applied Sciences, University of Wisconsin - Green Bay
Uniform polyhedra have regular polygon faces and identical vertices. The only convex uniform polyhedra are the five Platonic solids and the 13 Archimedean solids. If we expand the definition to allow interpenetrating faces, we obtain the four Kepler-Poinsot polyhedra and 53 others, for a total of 75.
Convex Uniform polyhedra
The Platonic Solids

The Archimedean Solids
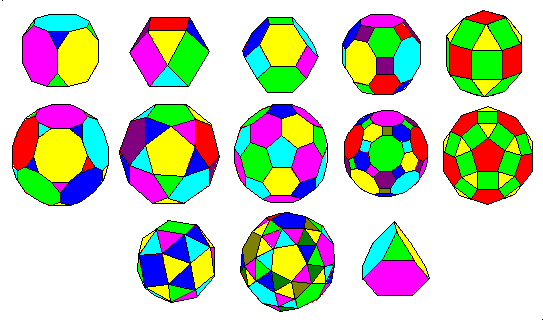
Non-convex Uniform polyhedra
The Kepler-Poinsot Solids


The Coxeter-skilling Non-convex Uniform polyhedra

Solids where faces pass through the center are sometimes called hemihedra. These and some other polyhedra can be considered "one-sided" since both sides of some faces are exposed at various times.


The solids above are derived from the rhombicuboctahedron and rhombicosidodecahedron by faceting, or removing parts of the solid bounded by planes within the solid.


The solids above are derived by faceting the cube and dodecahedron to produce 8/3 and 10/3 faces.


The solids above are derived from the rhombicuboctahedron and rhombicosidodecahedron by faceting, or removing parts of the solid bounded by planes within the solid.


The solids above are derived by faceting the cube and dodecahedron to produce 8/3 and 10/3 faces.

The two solids above have the same vertices and edges as the preceding two pairs, but the 8/3 and 10/3 faces have been faceted to result in intricate rosettes.

The three solids above result from faceting the square faces of a rhombicosidodecahedron


Faceting a dodecahedron results in a family of star-faced polyhedra

The solids above are derived by truncating the great dodecahedron, great icosahedron and great stellated dodecahedron







Snubs







The two solids above have the same vertices and edges as the preceding two pairs, but the 8/3 and 10/3 faces have been faceted to result in intricate rosettes.

The three solids above result from faceting the square faces of a rhombicosidodecahedron


Faceting a dodecahedron results in a family of star-faced polyhedra

The solids above are derived by truncating the great dodecahedron, great icosahedron and great stellated dodecahedron







Snubs






References
- Coxeter, H.S.M, Longuet-Higgins, M.S. and Miller, J.C.P., 1953, Uniform polyhedra, Philosophical Transactions of the Royal Society of London, v. A246, pp. 401-440.
- Wenninger, M. J., 1971, polyhedron Models, Cambridge University Press
- Skilling, J., 1975, The Complete Set of Uniform polyhedra, Philosophical Transactions of the Royal Society of London, v. A278, pp. 111-135.
Return to Symmetry Index
Return to Professor Dutch's Home page
Created 8 Oct. 1997, Last Update 2 March 1999